Obsah
Geometrická představivost
U starořeckých matematiků byla geometrie skutečnou výstavní síní matematiky. Dodnes nás udivuje, jakých výsledků bylo tehdy dosaženo. Samozřejmě, že geometrie se nadále rozvíjí ohromným tempem a její úloha je nezastupitelná. Přesto se zdá, že v dnešní době se částečně stáhla do ústraní, učebnice matematiky i odborné publikace plní spíše symboly, výrazy a rovnice než obrázky. I ve středoškolské praxi je však vhodné se občas vrátit ke geometrickým kořenům, může nás to jen obohatit.
Algebraické výrazy
Přestože se jedná o triviální záležitost, znovu a znovu se přesvědčujeme, že i násobení dvojčlenů může gymnazistům působit obtíže. Přitom geometrická interpretace je tak názorná.
(a + b)2 = a2 + 2ab + b2
 Obrázek sotva potřebuje další komentář. Výraz pro součin dvou různých dvojčlenů
Obrázek sotva potřebuje další komentář. Výraz pro součin dvou různých dvojčlenů
(a + b).(c + d) = ac + ad + bc + bd.
lze odvodit geometrickými prostředky velmi podobně, na jedné straně (nyní již) obdélníka naneseme délky c a d a rozložíme na čtyři obecně různé obdélníky.
(a – b)2 = a2 – 2ab + b2
Při geometrickém odvození tohoto vztahu vyjděme ze čtverce o straně a (na obrázku modře).
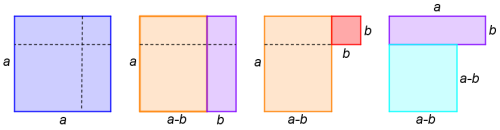 Nyní od něj odřízněme obdélník šířky b (fialově) a zůstane oranžová část. Abychom nyní mohli odříznout další obdélník o stranách a a b podle čárkované meze, musíme přidat (červený) čtverec o straně b. Po odříznutí požadovaného obdélníka nám zůstane tyrkysový čtverec, jehož strana je a – b. Provedeme nyní bilanci: vložili jsme čtverec obsahu a2 a čtverec obsahu b2, odřízli jsme dva obdélníky obsahu ab a zbyl nám čtverec obsahu (a – b)2. To odpovídá zkoumanému vzorci.
Nyní od něj odřízněme obdélník šířky b (fialově) a zůstane oranžová část. Abychom nyní mohli odříznout další obdélník o stranách a a b podle čárkované meze, musíme přidat (červený) čtverec o straně b. Po odříznutí požadovaného obdélníka nám zůstane tyrkysový čtverec, jehož strana je a – b. Provedeme nyní bilanci: vložili jsme čtverec obsahu a2 a čtverec obsahu b2, odřízli jsme dva obdélníky obsahu ab a zbyl nám čtverec obsahu (a – b)2. To odpovídá zkoumanému vzorci.
(a + b).(a – b) = a2 – b2
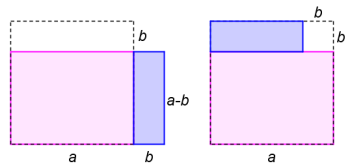 Obdélník na levé části obrázku (částečně vybarvený purpurově a částečně modře) má strany a + b a a – b. Čárkovaně je vyznačen čtverec o straně a. Ani po vhodném přesunutí modré části (viz pravá část) není tento čtverec zcela zaplněn. Chybějící část je právě čtverec o straně b. Obsah výchozího obdélníka je tedy roven rozdílu a2 – b2.
Obdélník na levé části obrázku (částečně vybarvený purpurově a částečně modře) má strany a + b a a – b. Čárkovaně je vyznačen čtverec o straně a. Ani po vhodném přesunutí modré části (viz pravá část) není tento čtverec zcela zaplněn. Chybějící část je právě čtverec o straně b. Obsah výchozího obdélníka je tedy roven rozdílu a2 – b2.
Kvadratická rovnice
Také nalezení kořenu kvadratické rovnice lze v jistém případě geometricky znázornit.
Na hliněných tabulkách babylonských učenců bychom mohli nalézt i návod k řešení takovéto úlohy: Nalezněte stranu čtverce tak, aby se celková plocha tohoto čtverce zvětšená o obdélník stejné výšky a zadané šířky rovnala ploše jiného zadaného obrazce. 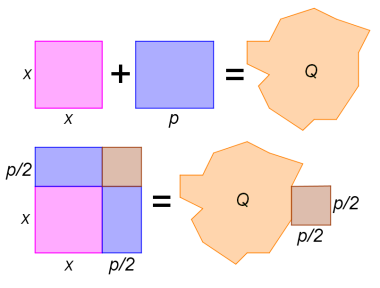 Dnes bychom text zadání pravděpodobně přepsali do podoby
Dnes bychom text zadání pravděpodobně přepsali do podoby
x2 + p.x = Q,
což je kvadratická rovnice pro neznámou x, kterou umíme snadno vyřešit pomocí známého vzorce.
Řešení je zaznamenáno v tomto duchu: Rozděl šířku obdélníka na polovinu, sestroj její pomocí čtverec a ten přidej k zadanému obrazci. Nyní sestroj čtverec o stejné ploše jako právě spojené útvary. Odečtením poloviny šířky obdélníka od jeho strany nalezneš hledanou délku. Ověřit správnost postupu řešení pomocí přiloženého obrázku je snadné. Symbolický zápis (nám pravděpodobně bližší) by vypadal takto
x = [Q + (p/2)2]1/2 – p/2
a není obtížné ověřit, že při použití notace v zadání odpovídá našemu běžnému vzorci.1)
Geometrické důkazy
V geometrii samotné (zvláště pak v planimetrii) je možné provést důkaz řady tvrzení velmi názorně a prakticky beze slov.
Pythagorova věta, která svazuje délku přepony c s délkami odvěsen a a b v pravoúhlém trojúhelníku vztahem a2+b2=c2, se dokazuje mnoha způsoby. Jeden méně obvyklý je ukázan na obrázku.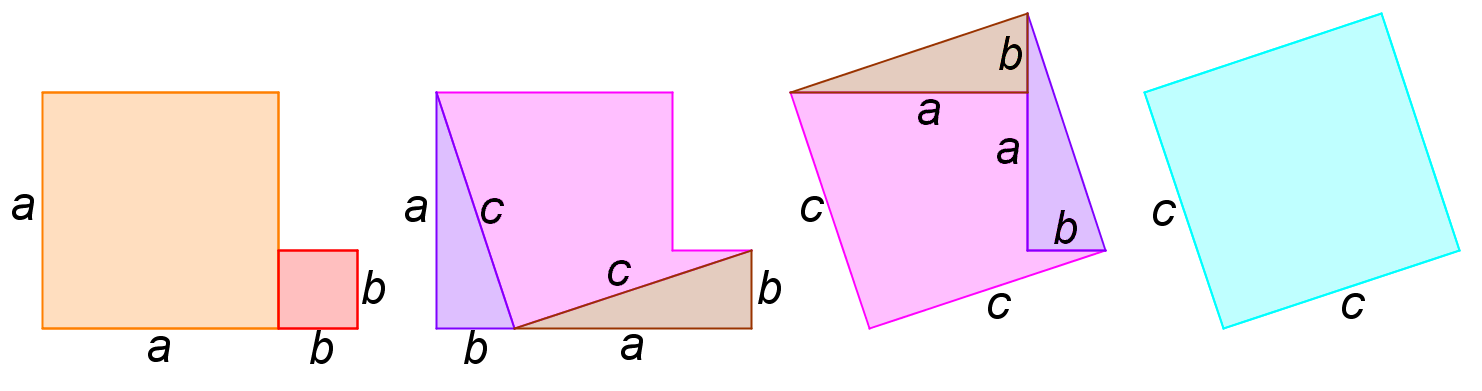
Obsah obecného trojúhelníka lze vypočítat mimo jiného i jako součin poloviny jeho obvodu s=(a+b+c)/2 a poloměru jemu vepsané kružnice r. K důkazu tvrzení S=r.s pomocí přeskládání vnitřních trojúhelníků opět asi není třeba žádný bližší popis.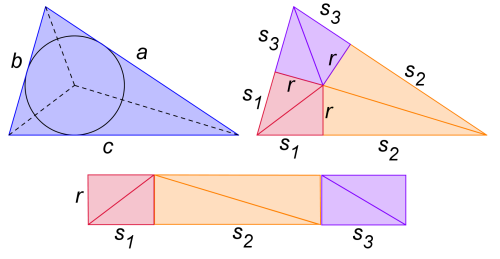
Goniometrické identity
S pomocí vhodného obrázku může být důkaz řady goniometrických vztahů hračkou.
Dobrým příkladem mohou být vztahy pro součet sinů nebo kosinů dvou úhlů, kterých se žáci často obávají:
sin α + sin β = 2.sin[(α + β)/2].cos[(α – β)/2]
cos α + cos β = 2.cos[(α + β)/2].cos[(α – β)/2]
Pro jejich důkaz si vytvoříme následující obrázek.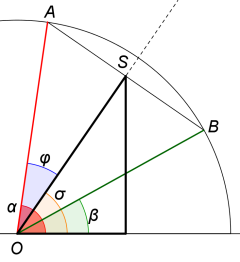 Okolo bodu O nakreslíme jednotkovou kružnici, na které vyznačíme body A a B. Jejich spojnice s počátkem svírají se zvoleným směrem úhly α a β. Souřadnice bodů tedy jsou A:[cos α; sin α], B:[cos β; sin β] a pro střed úsečky AB pak S:[(cos α + cos β)/2; (sin α + sin β)/2].
Okolo bodu O nakreslíme jednotkovou kružnici, na které vyznačíme body A a B. Jejich spojnice s počátkem svírají se zvoleným směrem úhly α a β. Souřadnice bodů tedy jsou A:[cos α; sin α], B:[cos β; sin β] a pro střed úsečky AB pak S:[(cos α + cos β)/2; (sin α + sin β)/2].
Z obrázku dále odvodíme, že pro úhel σ platí σ=(α + β)/2 a pro úhel φ pak φ=(α – β)/2, neboť je polovinou úhlu v rovnoramenném trojúhelníku AOB při vrcholu O. V pravoúhlém trojúhelníku AOS s přeponou délky 1 má odvěsna OS délku cos φ a z černě vytaženého pravoúhlého trojúhelníku pak už snadno můžeme vyjádřit souřadnice bodu S jako [cos σ.cos φ; sin σ. cos φ]. Nyní porovnáme obě vyjádření souřadnic bodu S pro y-ovou i x-ovou složku
(sin α + sin β)/2 = sin σ.cos φ
(cos α + cos β)/2 = cos σ.cos φ
a po vynásobení dvěma a dosazení za σ a φ již dostaneme hledané součtové vzorce.
Tangenty Rozdělíme-li pravý úhel na tři libovolné části α, β a γ, tj. α+β+γ=π/2, pak platí identita
tg α.tg β + tg β.tg γ + tg γ.tg α = 1.
Její odvození překvapivě není příliš náročné, stačí využít vhodný obrázek a vztahy pro goniometrické funkce v pravoúhlém trojúhelníku. Uvážíme, že levá strana obdélníka má délku 1 a postupně počítáme: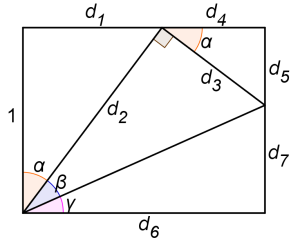
- d1 = tg α
- d2 = 1/cos α
- d3 = d2.tg β = tg β/cos α
- d4 = d3.cos α = tg β
- d5 = d4.tg α = tg α.tg β
- d6 = d1 + d4 = tg α + tg β
- d7 = d6.tg γ = tg α.tg γ + tg β.tg γ
Nyní si již pouze povšimneme, že d5 + d7 = 1 a po dosazení již máme hledanou identitu.
Číselné řady
Geometricky lze přiblížit i některé vzorce pro sčítání konečných číselných řad, které se obyčejně dokazují matematickou indukcí.
1 + 2 + 3 + 4 + … + n = n(n + 1)/2
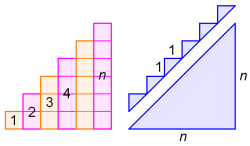 Součet prvních n přirozených čísel snadno získáme dle obrázku. Každý sčítanec si představíme jako příslušný počet jednotkových čtverců a vhodně je uspořádáme. Na vzniklý útvar se nyní podíváme jinýma očima. Představíme si jej jako pravoúhlý trojúhelník (polovina čtverce o straně n), přičemž jsme „odsekli“ celkem n malých trojúhelníčků (každý je polovinou jednotkového čtverce). Celkový plošný obsah tedy je S = n2/2 + n/2 a tedy S = n(n + 1)/2.
Součet prvních n přirozených čísel snadno získáme dle obrázku. Každý sčítanec si představíme jako příslušný počet jednotkových čtverců a vhodně je uspořádáme. Na vzniklý útvar se nyní podíváme jinýma očima. Představíme si jej jako pravoúhlý trojúhelník (polovina čtverce o straně n), přičemž jsme „odsekli“ celkem n malých trojúhelníčků (každý je polovinou jednotkového čtverce). Celkový plošný obsah tedy je S = n2/2 + n/2 a tedy S = n(n + 1)/2.
1 + 3 + 5 + 7 + … + (2n – 1) = n2
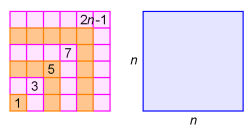 Součet n prvních lichých čísel je roven čtverci jejich počtu. Znovu každé číslo reprezentujeme příslušným počtem jednotkových čtverců, které skládáme dle obrázku. Je zřejmé, že každé následující číslo má přesně správný počet „cihliček potřebných k obestavění“ dvou stran stávajícího čtverce (to vlastně odpovídá indukčnímu kroku při tradičním způsobu důkazu).
Součet n prvních lichých čísel je roven čtverci jejich počtu. Znovu každé číslo reprezentujeme příslušným počtem jednotkových čtverců, které skládáme dle obrázku. Je zřejmé, že každé následující číslo má přesně správný počet „cihliček potřebných k obestavění“ dvou stran stávajícího čtverce (to vlastně odpovídá indukčnímu kroku při tradičním způsobu důkazu).
13 + 23 + 33 + … + n3 = (1 + 2 + 3 + … + n)2
I tento krásný vztah byl dokázán již starořeckými matematiky, není však známo, že by použili následující geometrickou konstrukci.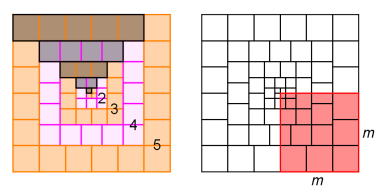 Vezměme čtyři jednotkové čtverce a složme z nich čtverec o straně 2. Ten nyní obestavíme čtverci o straně 2. Opět vznikne čtverec, který obestavíme čtverci se stranou 3. Takto pokračujeme až k zadanému n. Situaci můžeme vidět na obrázku. Obsah čtverce můžeme vyjádřit jako 4.1.12 + 4.2.22 + 4.3.32 + … + 4.n.n2. Každou novou vrstvu můžeme složit pomocí čtyř stejných obdélníků, každý z nich má právě tolik čtverců jaká je délka jejich strany). Tyto obdélníky jsou znázorněny jako šedé podbarvení na levém obrázku. Výraz pro obsah čtverce můžeme upravit na 4.(13 + 23 + 33 + … + n3). Při pohledu na pravý obrázek je však zřejmé, že obsah čtverce může být vyjádřen také jako čtyřnásobek obsahu červeného čtverce. Jeho strana je m = 1 + 2 + 3 + … + n a jeho obsah tedy m2 = (1 + 2 + 3 + … + n)2. Porovnáním obou vyjádření obsahu velkého čtverce již dostáváme požadovaný vztah.
Vezměme čtyři jednotkové čtverce a složme z nich čtverec o straně 2. Ten nyní obestavíme čtverci o straně 2. Opět vznikne čtverec, který obestavíme čtverci se stranou 3. Takto pokračujeme až k zadanému n. Situaci můžeme vidět na obrázku. Obsah čtverce můžeme vyjádřit jako 4.1.12 + 4.2.22 + 4.3.32 + … + 4.n.n2. Každou novou vrstvu můžeme složit pomocí čtyř stejných obdélníků, každý z nich má právě tolik čtverců jaká je délka jejich strany). Tyto obdélníky jsou znázorněny jako šedé podbarvení na levém obrázku. Výraz pro obsah čtverce můžeme upravit na 4.(13 + 23 + 33 + … + n3). Při pohledu na pravý obrázek je však zřejmé, že obsah čtverce může být vyjádřen také jako čtyřnásobek obsahu červeného čtverce. Jeho strana je m = 1 + 2 + 3 + … + n a jeho obsah tedy m2 = (1 + 2 + 3 + … + n)2. Porovnáním obou vyjádření obsahu velkého čtverce již dostáváme požadovaný vztah.
Poznámka: Stranu velkého čtverce lze kromě dvojnásobku m vyjádřit také pomocí n + 1 čtverců o straně n, tj. n(n + 1). Srovnáním těchto veličin dostaneme již dříve uvedený vztah pro součet n prvních přirozených čísel ještě jiným způsobem.
Na závěr tedy dovolte malé doporučení: Při řešení matematických úloh si kreslete obrázky a náčrty, často vám mohou pomoci při řešení, hlubším pochopení souvislostí i snazším zapamatování!
Literatura
- Krocení nekonečna - příběh matematiky od prvních čísel k teorii chaosu, Ian Stewart, CPress (2014)
- Wolfram MathWorld, Eric W. Weisstein
- Heron's Formula via Proofs Without Words, Roger B. Nelson, College Mathematics Journal 32 (2001), no. 4
- Umění programování, díl 1. Základní algoritmy, D. E. Knuth, Computer press (2008)