Funkce

Věnovali jsme poměrně hodně času, abychom s pomocí příkladů z různých oborů matematiky důkladně procvičili používání podmínek a cyklů v rozličných situacích. Vytvářené programy byly rozsahem velmi malé a jejich struktura nebyla příliš komplikovaná.

Pokud chceme postupně dospět k řešení i trochu komplikovanějších úloh, musíme se efektivně vyrovnat s dvěma úkoly:

1. opakované použití části kódu na různých místech programu, případně i v jiných programech,
2. vhodné rozdělení monolitického programu do menších bloků, které jsou snáze srozumitelné, lépe se píší i testují a mohou být souběžně vyvíjeny různými programátory.

Odpovědí programovacích jazyků (tj. nejen Pythonu) na tyto potřeby je koncept funkce (případně v některých jazycích též podprogramu). Pod funkcí budeme rozumět blok relativně samostatného kódu sloužící k provedení určité požadované činnosti.

Pro vykonání této činnosti provedeme volání funkce, podle potřeby volané funkci předáme parametry, kterými ovlivňujeme její činnost. Funkce pak může pomocí návratové hodnoty předat zpět výsledky své činnosti, zároveň může provádět i jinou (navenek zjistitelnou) činnost (např. tisknout do konzole, číst či zapisovat do souboru, komunikovat pomocí sítě, zajišťovat časovou prodlevu atp.). Z uvedeného plyne, že volání funkce je dalším případem, kdy dochází k porušení přirozeného sledu příkazů. K použití funkce může dojít i opakovaně (se stejnými či rozdílnými parametry). Až po dokončení kódu uvnitř funkce dojde k návratu zpět a zpracování dalšího příkazu za voláním funkce. 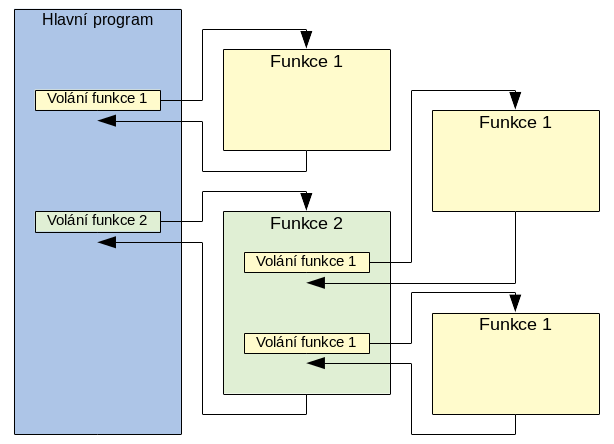Ilustrovat se to snaží obrázek, kde kromě bloku hlavního programu máme ještě dvě různé funkce. První z nich je volána opakovaně (jednou přímo z hlavního programu, dvakrát z druhé funkce), druhá jen z jednoho místa hlavního programu. Šipkami je znázorněno předání řízení mimo obvyklé pořadí příkazů.

Prakticky ve všech našich dosavadních programech jsme již funkce využívali. Jedná se o funkci input pro načtení řetězce z terminálu a o funkci print pro výstup na terminál, jejich pomocí naše programy vlastně komunikují s obsluhou. Nedávno jsme si představili funkci range pro využití v cyklu for. Vzhledem k tomu, že nám to nečinilo žádné zásadní potíže, předpokládám, že koncept funkce se nám jeví poměrně přirozený a snadno pochopitelný.

Při použití funkcí jsme nevěděli nic o tom, jak jsou implementované, a na druhou stranu jejich autoři nemohli dopředu vědět nic o našich programech, které jejich funkce budou používat. To je v praxi ona výše zmíněná samostatnost jednotlivých funkcí. Volající kód a kód funkce tvoří dva oddělené světy, které spolu interagují pomocí parametrů funkce a návratové hodnoty¹⁾.

Python již ve svém základu má vestavěny některé funkce pro běžné činnosti, množství dalších je dostupných pomocí modulů (jakýchsi sad či knihoven funkcí), některé moduly jsou součástí základní distribuce jazyka, jiné se musí zvlášť doinstalovat. Samozřejmě, že programátoři si běžně při vývoji programu vytvářejí vlastní funkce (to si také brzy ukážeme a budeme důkladně procvičovat).

Funkci voláme pomocí jejího jména, za ním do kulatých závorek uvádíme seznam parametrů předaných funkci. Mohou to být konstanty, proměnné nebo i výrazy.

print(jmeno_a_prijmeni)              # volání funkce s jedním parametrem
print()                              # volání funkce bez parametrů
print("T =", konec - zacatek, "s")   # tři parametry oddělené čárkou

Návratovou hodnotu funkce můžeme přiřadit do proměnné nebo použít ve výrazu (případně ji můžeme ignorovat).

vstup = input("Zadej číslo:")

Počet parametrů funkce a jejich možný datový typ je určen programátorem funkce. Funkce print nemusí mít žádný parametr nebo jich může být několik, přičemž jejich typ není striktně určen. Funkce range může mít jeden, dva nebo tři parametry typu int, funkce input může mít nejvýše jeden parametr typu str (řetězec). Na pořadí těchto parametrů (někdy se hovoří o pozičních parametrech) záleží.

Kromě pozičních parametrů může funkce mít ještě pojmenované (též klíčové parametry). Ty mají tvar jméno = hodnota a uvádějí se vždy až za pozičními parametry. Jejich použití při volání funkce je nepovinné. Programátor totiž při implementaci takového parametru definuje přednastavenou hodnotu, která nahradí chybějící parametr při volání funkce.

Funkce print umožňuje předefinovat oddělovač použitý mezi výstupem více hodnot pomocí pojmenovaného parametru sep, který je přednastaven na jednu mezeru.

a, b, c = 1, 2, 3                     # inicializace proměnných
print(a, b, c)                        # => 1 2 3
print(a, b, c, sep = ",")             # => 1,2,3
print(a, b, c, sep = " - ")           # => 1 - 2 - 3

Dále je možné předefinovat ukončovač (to, co se vytiskne za poslední hodnotou) pomocí parametru end (přednastavená hodnota je odřádkování).²⁾

print(a, b, end = "***")        
print(c)                              # => 1 2***3 (s odřádkováním)

Parametry sep a end jsou řetězce, mohou být uvedeny i současně, pak na jejich pořadí nezáleží (ale oba musí následovat až za pozičními parametry).

print(a, b, c, sep = "_", end = "!")  # => 1_2_3! (bez odřádkování)

V Pythonu má každá funkce návratovou hodnotu. Pokud programátor žádnou neurčí a nepřiřadí, použije se speciální hodnota None (tj. nic) datového typu NoneType (žádný typ), což prakticky znamená „bez návratové hodnoty“ (ale je možné např. takový stav otestovat v podmínce). Návratová hodnota funkce print je právě None, funkce input vrací řetězec zadaný uživatelem (typ str).

Již dříve jsme se seznámili s některými funkcemi, které jsou přímo vestavěny do jazyka Python, a běžně jsme je používali ve svých programech. Kromě již zmíněných input, print a range jsou to funkce pro změnu datového typu:

• int převede argument (tj. skutečně předaný parametr) na celočíselnou hodnotu (pokud to je možné),
• float vrací číslo s plovoucí desetinnou čárkou,
• str převede argument do textové podoby,
• bool určí logickou hodnotu výrazu.

int(2.8)               # => 2, float => int
int('25')              # => 25, str => int
int(True)              # => 1, bool => int
float('+infinity')     # => inf, str => float
str(True)              # => 'True', bool => str
bool('')               # => False, str => bool (prázdný řetězec)

Nyní se seznámíme s několika dalšími. Pro zjištění aktuálního datového typu proměnné či výrazu můžeme použít funkci type s jedním parametrem.

type(568)              # => <class 'int'>
type(12 / 2)           # => <class 'float'>, reálné dělení!
type(not True)         # => <class 'bool'>

Délku řetězce (a později uvidíme, že i počet položek dalších datových kontejnerů) nám vrátí funkce len.

len('')                # => 0, prázdný řetězec
len('krátký text')     # => 11 znaků

Absolutní hodnotu číselného výrazu nám vrátí funkce abs a pomocí funkce round zaokrouhlíme číselný výraz (na celé číslo nebo pomocí druhého parametru typu int na daný počet desetinných míst).

abs(-4)                # => 4, int
abs(-4.85)             # => 4.85, float
round(4.12)            # => 4, int
round(-4.65)           # => -5, int
round(1.66666666, 3)   # => 1.667, float (na 3 desetinná místa)

Pro nalezení největší a nejmenší z několika hodnot nabízí Python funkce max a min.

max(1, 2, -2, 1.38)    # => 2
min(1, 2, -2, 1.38)    # => -2
max('a', 'b', 'c')     # => 'c', porovnávat lze nejen čísla

Python je univerzální programovací jazyk, který lze použít pro nejrůznější úlohy. Proto již jeho standardní distribuce zahrnuje mnoho modulů, které poskytují specializované funkce a objekty pomáhající programátorům tyto úlohy řešit. Množství dalších modulů je možné si stáhnout a doinstalovat, řada z nich je prakticky nedílnou součástí ekosystému jazyka a je de facto standardem. Stejně jako funkce je možné vytvářet si vlastní moduly a ty sdílet s dalšími programátory.

Rozdělení do modulů nám umožňuje na jedné straně udržet si přehled a pořádek, na druhé straně to zefektivňuje a zrychluje práci kompilátoru jazyka. Jako příklady standardních modulů si můžeme uvést math poskytující běžné matematické funkce, random pro práci s pseudonáhodnými čísly nebo datetime pro práci s časovými daty v programech. Z externích modulů jsme se (byť jen okrajově) setkali např. s knihovnou na vytváření grafů matplotlib.

Jako příklad si ukážeme využití modulu math, který umožňuje provádět výpočty exponenciální a logaritmické funkce, funkcí goniometrických a k nim inverzních cyklometrických a některých dalších.

import math         # zpřístupnění modulu
 
math.e              # => 2.718281828459045, Eulerovo číslo
math.exp(2)         # exponenciální funkce
math.log(10.0)      # přirozený logaritmus 
math.log(100, 3)    # logaritmus o základu 3
math.log2(16)       # => 4.0, logaritmus o základu 2
math.log10(0.01)    # => -2.0, dekadický logaritmus
 
math.pi             # => 3.141592653589793, Ludolfovo číslo
math.sin(math.pi/2) # => 1.0, sinus - argument v radiánech!
math.cos(math.pi/4) # kosinus
math.tan(math.pi/4) # tangens
math.asin(0.5)      # arkus sinus
math.acos(0.0)      # arkus kosinus
math.atan(1.0)      # arkus tangens
math.radians(180)   # převod úhlových stupňů na radiány
math.degrees(1.0)   # převod radiánů na úhlové stupně
 
math.sqrt(2)        # reálná odmocnina

Nejprve si musíme pomocí direktivy import modul zpřístupnit (stačí před prvním použitím, ale je dobrým zvykem to udělat hned na začátku programu). Na proměnné, funkce a případně další objekty modulu pak odkazujeme pomocí tečkové notace modul.objekt. Jinak se jejich použití neliší od jiných funkcí, počet a typ parametrů i návratové hodnoty nalezneme v dokumentaci, stejně tak jako další poznámky³⁾.

Pokud nějakou funkci (nebo několik málo) z modulu používáme v rámci svého programu velmi často, může být používání tečkové notace nepraktické. Je možné to obejít buď importem pouze dotčené funkce či objektu (objektů), např.

from math import pi, sin
print(sin(pi / 2))    # => 1.0

nebo přiřazením vlastních jmen dotčeným objektům

import math
sin = math.sin        # 'sin' je nyní nové lokální jméno
cislo_pi = math.pi
print(sin(cislo_pi))  # => 0.0

Lze udělat i import všech objektů modulu do lokálního prostoru jmen pomocí

from math import *

ale právě pro snížení přehlednosti a možné konflikty různých jmen se to nedoporučuje!