Obsah

Úlohy k procvičování

Programování se sotva lze naučit bez …ehm, programování. Pro zdokonalení a ověření svých znalostí můžete využít i následující úlohy. Nejedná se o žádné velmi náročné úkoly, přesto však jejich řešení může vyžadovat jisté netriviální úsilí.

Procházka po spirále

Ze čtvercových dlaždic označených nějakým symbolem sestavíme obdélníkové (případně čtvercové) pole. Naším úkolem je projít všechny dlaždice z levého horního rohu po spirále ve směru hodinových ručiček tak, jak je naznačeno na obrázku. 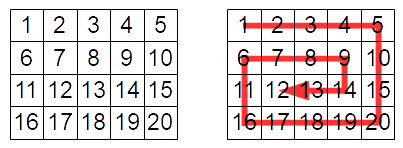procházka Napište funkci, která projde zadaným způsobem pole a vytvoří seznam dlaždic v pořadí, v jakém byly navštíveny. Vstupním parametrem funkce je dvojrozměrné pole (seznam seznamů), jednotlivé prvky mohou být čísla (jako na obrázku), ale i písmena apod.

Po vypracování a odladění funkce pro obecný případ pole dlaždic můžete zkusit upravit funkci tak, že vstupní parametry budou pouze počet řádků a počet sloupců. Budeme předpokládat, že dlaždice jsou číslovány přirozenými čísly od 1 výše (po řádcích, viz obrázek), reprezentaci dat dvojrozměrným polem tedy vůbec nebudeme potřebovat. Výsledkem funkce by měl být seznam přirozených čísel postupně navštívených dlaždic v průběhu procházky.

Snažte se postihnout i mezní případy (např. pouze 1 sloupec), při nekorektním zadání (nulový či záporný počet sloupců či řádků) by funkce měla vrátit prázdný seznam.

Audioaktivní posloupnost

Mějme nějaké přirozené číslo (např. 335) a na jeho základě budeme vytvářet posloupnost dalších členů takto:

Tuto myšlenku poprvé publikoval britský matematik John H. Conway v roce 1986, který vlastnosti takto tvořených posloupností také z matematického hlediska studoval. Podařilo se mu dokázat řadu často překvapivých skutečností, např. že pro libovolné počáteční přirozené číslo (s jedinou výjimkou1)) vytvářené členy nakonec narůstají nade všechny meze a dokonce že poměr délek dvou následujících členů se blíží univerzální hodnotě λ ≈ 1,30357727 (což je jediný reálný kořen jistého polynomu 71. stupně). Více informací naleznete na internetu, např. na anglické Wikipedii.

Vytvořte funkci aa_posloupnost, která na základě předaných parametrů zacatek (nultý člen posloupnosti jako přirozené číslo) a clenu (počet vygenerovaných členů posloupnosti) vypíše spolu s počátečním určený počet dalších členů audioaktivní posloupnosti, např. při volání funkce aa_posloupnost(71, 10) bude výstup vypadat takto. 

71
1711
111721
31171211
132117111221
1113122117312211
31131122211713112221
132113213221171113213211
111312211312111322211731131211131221
3113112221131112311332211713211311123113112211
13211321322113311213212322211711131221133112132113212221

Vzhledem ke skutečnosti, že tvoření členů posloupnosti probíhá na základě grafické reprezentace čísla (spíše než přímo podle číselné hodnoty), je vhodné uchovávat členy jako řetězce. Pro výpočet dalšího členu si patrně vytvoříte další pomocnou funkci, která bude zpracovávat jednotlivé znaky stávajícího členu a její návratovou hodnotou bude jeho následník (opět jako řetězec).

Hra na život

I tato úloha je spojena se jménem Johna H. Conwaye, který ji představil veřejnosti v roce 1970 a v jisté době se těšila široké popularitě a zájmu.

Představte si čtvercovou síť, kde každá buňka (tj. jeden ze základních čtverců) může být ve dvou stavech - bez života nebo obsahovat život. Celá dvojrozměrná síť se v čase vyvíjí podle jednoduchých pravidel2):

Za sousedy buňky považujeme nejbližších osm buněk, které se dané buňky dotýkají (jednou stranou nebo alespoň rohem). 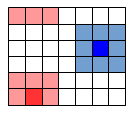sousedící buňky Pokud je síť, se kterou pracujeme, omezená, můžeme volit na okrajích různý postup. V našem případě budeme považovat buňky ležící na stejném řádku zcela vlevo a zcela vpravo za sousední (obdobně pro sloupce a dokonce i pro buňky v protilehlých rozích celého pole) - což bychom mohli označit za periodické okrajové podmínky. Na obrázku vpravo pak buňky označené tmavě modrou a tmavě červenou barvou mají po osmi sousedech vyznačených světlejším odstínem.

Podle popsaných pravidel určíme stav populace v další generaci. Nyní můžeme v cyklu tento proces opakovat a sledovat chování našeho systému (podobné systémy se nazývají buněčné automaty). Ukazuje se, že v závislosti na počátečních podmínkách (tj. stavu nulté generace) se vývoj může ubírat rozličnými směry - někdy populace rychle vyhyne, jindy se rychle nebo naopak až po mnoha generacích dostane do stabilního stavu a může se ukázat, že vývoj není nikdy ukončen. Pomocí počítačových simulací vznikly přímo „atlasy“ různých elementárních konfigurací se zajímavými vlastnostmi - tzv. zátiší (stabilní uspořádání), oscilátory s periodicky se opakujícími konfiguracemi, posunující se vzory, děla vystřelující posunující se projektily a řada dalších, viz např. česká Wikipedie. Změna v jediné buňce na počátku může vést k rapidnímu rozdílu ve vývoji populace. Je skutečně pozoruhodné, jakou mnohotvárností a složitostí se vyznačuje systém s takto jednoduchými pravidly. Příklad vývoje jednoduchého tvaru po tři generace ukazuje obrázek. 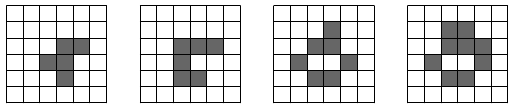vývoj R-pentomina Vaší úlohou bude vytvořit funkci pro simulaci života podle popsaných pravidel. Budeme předpokládat čtvercové pole (reprezentované v Pythonu seznamem seznamů se stejným počtem sloupců a řádků), stav buňky bude určen boolovskou hodnotou (True pro buňku se životem). Na původně prázdné pole umístíme několik živých buněk a v cyklu spustíme výpočet další generace. K tomu si vytvoříme prázdné pole stejné velikosti, postupně procházíme všechny buňky a určujeme, zda přežijí či v nich vznikne nový život. Výsledky zapisujeme do nového pole. Stav populace v každé generaci vytiskneme, např. takto (znak . pro buňky bez života a X pro živou). 

0. generace
......
......
...XX.
..XX..
...X..
......

Řešení je vhodné rozdělit na více funkcí, např. pro pro vytvoření prázdného pole, pro výpočet počtu živých sousedů určené buňky, pro výpočet následující generace, pro tisk pole, apod., a ty jednotlivě odladit. Pro jednoduchost můžete pracovat s polem přednastavené velikosti (např. o hraně 10 buněk), ale ponechte si možnost změnou jedné proměnné situaci podle potřeby měnit. To samé platí pro počet počítaných generací.

Výpočet zlomku

Výpočtem zlomku s „neomezenou přesností“ jsme se již zabývali, jedním ze způsobů bylo napodobení písemného dělení. Nyní si úlohu doplníme o podmínku, že v desetinné části výsledku nalezneme periodicitu, pokud se vyskytuje.

Mějme tedy dvě přirozená čísla citatel a jmenovatel, úkolem bude napsat funkci se dvěma parametry zlomek(citatel, jmenovatel), která vrátí desetinný zápis hodnoty zlomku jako řetězec. Případná perioda v desetinné části bude uzavřena do hranatých závorek, jak je vidět níže. 

zlomek(20, 5)              => "4"
zlomek(17, 8)              => "2.125"
zlomek(4, 3)               => "1.[3]"       # tj. 1.33333333...
zlomek(1, 60)              => "0.01[6]"     # tj. 0.01666666...
zlomek(5, 11)              => "0.[45]"      # tj. 0.45454545...
zlomek(3, 7)               => "0.[428571]"

Při řešení opět vyjděte z metody písemného dělení a rozmyslete si, za jakých podmínek vzniká periodicita v desetinné části a za jakých okolností je zlomek vyčíslen přesně. :!: Pouhé opakování nějaké číslice ve výsledku ještě nemusí nutně znamenat, že je nalezena perioda (v příkladu níže se každá číslice uvnitř periody vyskytuje alespoň dvakrát). 

zlomek(213, 230)           => "0.9[2608695652173913043478]"

Římské číslice

Napište funkce pro vzájemný převod čísel zapsaných pomocí běžných (arabských) a římských číslic, tj. vytvořte funkce 

def na_rimske(cislo):
    pass
 
def na_arabske(retezec):
    pass

Pro římský zápis použijte číslice I (s hodnotou 1), V (5), X (10), L (50), C (100), D (500) a M (1000), čímž lze vyjádřit všechna celá čísla v rozsahu 1 až 3999. Přitom respektujte běžná pravidla, tj. jeden symbol se smí opakovat maximálně třikrát po sobě a např. 9 vyjádříme jako IX. Římský zápis budeme uchovávat jako znakový řetězec.

Jednodušší je převod z běžného (arabského) tvaru do římského, opačný převod je o něco složitější. Můžete proto nejprve předpokládat, že parametr funkce na_arabske obsahuje platnou římskou reprezentaci čísla v povoleném rozsahu. Následně pak můžete přistoupit i k náročnější variantě, která dokáže odhalit i neplatné vstupní řetězce (např. IM, XCAIII, LIIIV) a případně vyvolá výjimku ValueError. Myslím, že vhodně připravené tabulky vám s vytvořeních požadovaných funkcí pomohou.

Zkontrolujte svoje funkce např. pomocí 

# testování správnosti převodu v obou směrech pro platný
# rozsah čísel (1 až 3999)
for cislo1 in range(1, 4000):
    rimsky = na_rimske(cislo1)
    cislo2 = na_arabske(rimsky)
    if cislo1 != cislo2:
        print("nesoulad:", cislo1, "-", rimsky)
print("test dokončen")

případně můžete ověřit i rozpoznávání nekorektních vstupú pomocí 

# dále testujeme rozpoznání nesprávných zápisů římskými číslicemi
test = ["IM", "XCAIII", "LIIIV", "M ", "", "-", "XIVII", "MMMM", "LD", "CXCXLII"]
for polozka in test:
    try:
        cislo = na_arabske(polozka)
        print("chyba:", polozka, "=>", cislo)
    except ValueError:
        pass
print("test dokončen")

Řešení

Úlohy byste se měli snažit vyřešit samostatně. Překonáváním překážek i procházením věhlasných Cimrmanových „slepých uliček“ se naučíte nejvíc, určitě se nejedná o ztracený čas. Níže uvedená řešení vám mohou posloužit jako příklad přístupu často odlišného od vašeho. Určitě nelze tvrdit, že zde uvedený kód je ideální či nejlepší, neboť se mj. vyhýbá neprobraným konstrukcím jazyka či optimalizovaným nástrojům v externích modulech. Někdy je kód z hlediska názornosti úmyslně „ukecanější“, než by musel být, a v neposlední řadě můžete zkrátka přijít na lepší řešení.

1)
Zkuste nalézt přirozené číslo, které vytváří audioaktivní posloupnost, ve které jsou všechny členy shodné.
2)
Pravidla jsou motivována tím, že životu se daří pouze v koloniích (nikoliv osamoceně), ale pokud koncentrace života přesáhne určitou mez, dojde k vyčerpání zdrojů a populace hyne.