O jednom jednoduchém poměrně užitečném tvrzení, které si nějak nenašlo cestu do středoškolských učebnic.

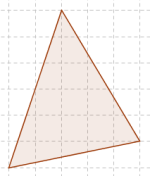Představme si jednoduchou úlohu. Máme zadán trojúhelník dle obrázku a úkolem je určit jeho obsah (přitom předpokládáme, že vyznačená mřížka určuje jednotkovou vzdálenost).

Vyzbrojeni znalostmi z analytické geometrie se už už chystáme vrhnout do výpočtů, když nám kdosi nahlédne přes rameno a během necelých pěti vteřin oznámí: obsah je 14.

Poté, co odezní prvotní ohromení, podíváme se znovu na zadání a uvědomíme si, že zadaný trojúhelník není zadán úplně obecně—všechny jeho vrcholy totiž leží v mřížových bodech. Brzy nám dojde, že toho se dá s výhodou použít, a pomalu si představujeme, jak trojúhelník rozřezáváme na kousky, které pak znovu skládáme vhodným způsobem, abychom získali celé „dlaždice“. Po jisté době také dojdeme ke shodnému výsledku bez dalších výpočtů, možná však budeme přeci jen potřebovat nějaký pomocný nákres. Přesto nám není jasné, jak náš rádce dospěl k výsledku tak rychle. Odpověď zní—použil Pickovu větu!

Znění uvedeného tvrzení je následující:

Jinými slovy: mřížový bod ležící uvnitř mnohoúhelníka přispívá k obsahu jedním mřížovým čtvercem, mřížový bod na jeho straně polovinou čtverce a nakonec musíme jeden čtverec odečíst.

Výsledek je v „mřížových čtvercích“, tj. má-li mřížka rozestupy 1 cm, obsah je v cm², má-li je 3 cm, musíme číselnou hodnotu S vynásobit vynásobit 9 cm².

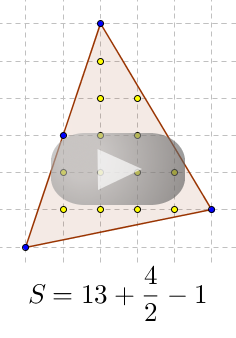
Podívejme se nyní, jak tuto novou větu použijeme na naše zadání.

Zadaný trojúhelník podmínky věty evidentně splňuje. Spočítáme tedy vnitřní mřížové body (je jich 13), mřížové body na stranách (tedy i ve vrcholech), které jsou 4, a po dosazení máme

Celý postup je velmi dobře patrný na přiložené animaci.

Nyní je tedy zřejmé, že rychlé výpočty obsahů některých mnohoúhelníků jen tak z hlavy nejsou žádná magie. 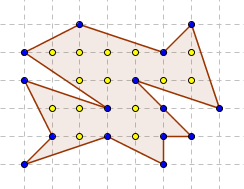Příště tak i vy můžete překvapit své okolí bleskovým řešením zdánlivě obtížné geometrické úlohy.

Nezapomeňte také, že Pickova věta platí pro všechny mnohoúhelníky, které splňují její podmínky, tedy kupříkladu i pro pro útvar na obrázku vlevo. 14 vnitřních a 15 stranových mřížových bodů určují S = 20,5.

Je poměrně překvapivé, že zmíněná věta byla poprvé publikována až roku 1899. Toto tvrzení tedy uniklo pozornosti řeckých matematiků, kteří zvláště v oblasti geometrie dosáhli ohromné množství výsledků, i řady jejich následníků.

Jejím objevitelem je rakouský matematik Georg Alexander Pick (1859-1942), který má úzký vztah k naší zemi. Po studiích a doktorátu na vídeňské univerzitě odešel roku 1880 do Prahy na německou Karlo-Ferdinandovu univerzitu jako asistent Ernesta Macha. Později zde i přednášel a zůstal s výjimkou krátké stáže v Lipsku až do konce své vědecké a pedagogické kariéry v roce 1927. Byl to G. Pick, který seznámil A. Einsteina s řadou matematických výsledků, které mu později umožnily formulovat své fyzikální teorie. Do Prahy se ze svého vídeňského důchodu znovu vrátil, ale za mnohem pochmurnějších okolností. Po obsazení Rakouska nacisty roku 1938 hledal kvůli svému židovskému původu útočiště v Čechách, ale nacisté ho po zřízení protektorátu přece dostihli a roku 1942 v terezínské pevnosti umírá.

• Podivuhodné křivky, počítání králíků a jiná matematická dobrodružství, Keith Ball, Argo/Dokořán (2011)
• Matematická kniha, Clifford A. Pickover, Argo/Dokořán (2012)
• Pickova věta a Georg Alexander Pick