Současná špičková matematika je natolik specializovaná a abstraktní záležitost, že i pro běžné vysokoškoláky např. technických směrů je nesmírně obtížné až prakticky nemožné sledovat a rozumět jejím nejnovějším výsledkům. Na druhé straně existují i velmi jednoduše formulované problémy přístupné široké veřejnosti, na jejichž řešení je zatím matematika krátká. Jedním z nich je tzv. Collatzova domněnka.

Budeme zkoumat posloupnosti přirozených čísel. Začneme libovolným takovým číslem (označme jej a₀) a každý následující člen vytváříme podle tohoto pravidla:

• je-li číslo a_i sudé, pak následuje a_i+1 = a_i / 2,
• je-li číslo a_i liché, pak následuje a_i+1 = 3.a_i + 1.

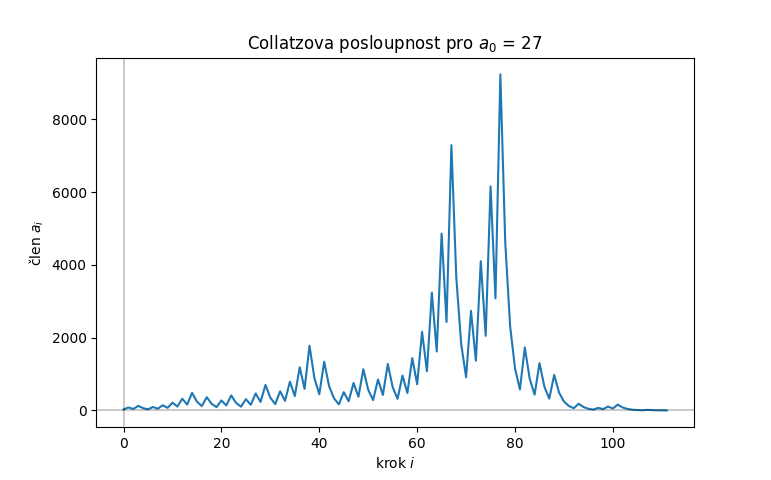
Proces vytváření dalšího členu přerušíme, pokud dosáhneme čísla 1. Počet kroků potřebných k dosažení 1 nazveme délkou Collatzovy posloupnosti. Např. při počátku 17 dostaneme posloupnost 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 s počtem kroků 12.

Pokud bychom pokračovali podle uvedeného pravidla, dostali bychom nekonečný cyklus 1 → 4 → 2 → 1 → 4 → atd., tudíž toto chování není pro nás zajímavé a do zkoumané posloupnosti ho nezahrnujeme. Ukazuje se, že přestože se pro mnohá počáteční čísla posloupnost chová poměrně „divoce“, vždy nakonec dosáhne konečné 1. Tedy vypadá to, že pro libovolné přirozené číslo nakonec dosáhne 1 (což je právě tvrzení Collatzovy domněnky), ale rigorózní matematický důkaz dosud chybí. Není totiž vyloučeno, že pro nějaké počáteční číslo posloupnost skončí v nějakém jiném nekonečném cyklu¹⁾ nebo neustále roste nade všechny meze. Zdá se dokonce, že matematici ani příliš netuší, jakými cestami by ke konečnému důkazu mohli dojít. Experimentálně byla na počítačích domněnka ověřena pro čísla až do 8.10⁸⁸, ale to není matematický důkaz a uvedené tvrzení stále zůstává pouhou domněnkou.

S pomocí jednoduchých programů se trochu seznámíme s některými vlastnostmi těchto podivuhodných posloupností. Pro zadané číslo vypíšeme posloupnost vytvořenou podle uvedených pravidel a určíme počet kroků k dosažení 1.

collatz1.py

# výpis Collatzovy posloupnosti pro zadané číslo
 
# vstup dat
a = int(input('Zadej počátek posloupnosti: '))
 
kroku = 0 # inicializace počítadla
 
# hledáme další člen posloupnosti než dosáhneme 1
while a != 1:
    if a % 2 == 0:
        a = a // 2 # další člen pro sudé číslo
    else:
        a = 3 * a + 1 # další člen pro liché číslo
    print(a) # tisk dalšího členu posloupnosti
    kroku = kroku + 1 # aktualizace počítadla
 
# tisk výsledku
print('Počet kroků v posloupnosti:', kroku)

Poznámka:
Říkali jsme si, že správně zapsaný algoritmus by neměl skončit v nekonečném cyklu, že to je chyba návrhu či implementace. V tomto případě vlastně nevíme, zda algoritmus nebude pro některý vstup provádět nekonečný cyklus. Na druhé straně případné vyvrácení Collatzovy domněnky (a trvalá sláva ve světě matematiky) za takový prohřešek proti pravidlům rozhodně stojí .

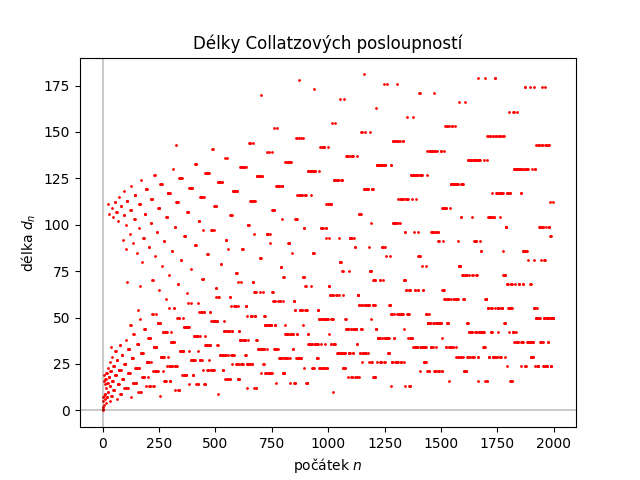
Pro hledání „zajímavých“ čísel (jejichž posloupnosti se výrazně odlišují od svých sousedů) můžeme program upravit tak, že v posloupnosti budeme také hledat její maximum, a následně již nebudeme vypisovat celou posloupnost, nýbrž jen její délku a dosažené maximum. To provedeme pro každý počátek v zadaném rozsahu. Jinými slovy: vytvoříme tabulku, kde na každém řádku bude počátek posloupnosti, její délka a dosažená maximální hodnota.

collatz2.py

# zkoumání vlastností Collatzovy posloupnosti v zadaném rozsahu
 
# vstup dat
cisel = int(input('Zadej maximální testované číslo: '))
 
# postupně pro jednotlivá čísla vytváříme posloupnosti
cislo = 1
while cislo <= cisel:
    a = cislo # počátek posloupnosti
    kroku = 0 # inicializace počítadla kroků
    max = a # pro uschování aktuálního maxima posloupnosti
    # hledáme další člen posloupnosti než dosáhneme 1
    while a != 1:
        if a % 2 == 0:
            a = a // 2 # další člen pro sudé číslo
        else:
            a = 3 * a + 1 # další člen pro liché číslo
        if a > max:
            max = a # aktualizace maxima
        kroku = kroku + 1 # aktualizace počítadla
 
    # tisk výsledku
    print(cislo, '- délka:', kroku, ', maximum:', max)
 
    cislo = cislo + 1 # další číslo ke zkoumání

S jeho pomocí například snadno zjistíme, že v rozsahu 1 až 30 je absolutním rekordmanem číslo 27 s délkou posloupnosti 111 a maximem 9232. Rozšíříme-li rozsah až do 50, pak délka 111 překonána není, ale pro další tři čísla dosáhnou posloupnosti stejného maxima 9232. O zajímavosti chování Collatzových posloupností vypovídají i následující grafy²⁾.