Ctrl a C.Za normálních okolností se jednotlivé příkazy programu vykonávají v pořadí jejich zápisu ve zdrojovém souboru. S výjimkou těch opravdu nejjednodušších úloh ale potřebujeme nástroje, které tuto následnost za určitých podmínek naruší a umožní rozhodování a opakování částí programu.
Dosud jsme pracovali s výrazy a proměnnými, které nabývaly číselných nebo textových hodnot. Pro vyhodnocení podmínek potřebujeme další datový typ, který určí splnění či nesplnění podmínky. Timto typem je bool (na památku G. Boola), jehož jediné možné hodnoty jsou True (pravda, splněno) a False (nepravda, nesplněno).
pravda = True # logická proměnná s hodnotou True lez = False # logická proměnná s hodnotou False # logické hodnoty vznikají jako výsledek aritmetických relací 12.0 > 5.4 # větší než => True -3.0 >= -3 # větší než nebo rovno => True 2 * 8 < 16 - 1e-5 # menší než => False 0.3333333333 <= 1/3 # menší než nebo rovno => True # rovnost používá '==' (na rozdíl od přiřazení '=') 0.33333333333333333 == 1/3 # => True (omezená přesnost typu float!) 0.33333 != 1/3 # nerovnost (je různé od) => True # ve složitějších logických výrazech používáme logické oprátory # and - True když platí oba výrazy zároveň # or - True když platí alespoň jeden z výrazů # not - negace platnosti 2 > 1 and 5 % 3 == 1 # => False 2 > 1 or 5 % 3 == 1 # => True not 12 > 5.4 # => False # priorita operátorů: not, and, or (v klesajícím pořadí), # v případě potřeby nebo pro přehlednost používáme závorky 2 == 2.0 and (not(pravda or lez) or True) # => True # lze použít i konstrukce s několika relačními operátory 0 < 1 < 2 < 3 < 4 # => True 0 == 0.0 == float('0') # => True # porovnávat lze i řetězce (ale problematika je složitější!) 'alfa' < 'omega' # => True 'alfa' < 'OMEGA' # velká písmena mají přednost => False 'ř' < 's' # neanglické znaky to komplikují => False '20' != '20.0' # řetězce! => True # v pohádkách a programování je určitě (v životě snad) pravda > lez # => True # v logickém kontextu mají hodnotu True # nenulová čísla bool(5.4) # => True bool(0) # => False # neprázdné řetězce bool('0') # => True bool('') # => False
Pomocí příkazu if lze dosáhnout změny v pořadí zpracování příkazů na základě výsledku vyhodnocení logického výrazu v podmínce. Základní možnosti jsou uvedeny ve formě vývojového diagramu na obrázku.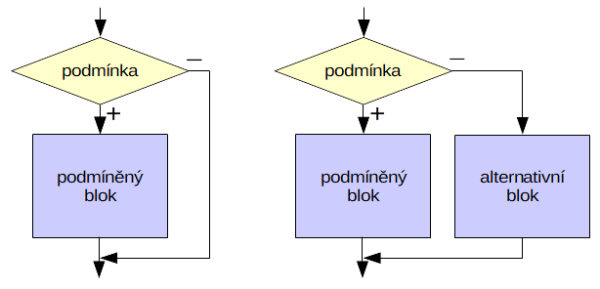 Každé situaci odpovídá fragment zdrojového kódu.
Každé situaci odpovídá fragment zdrojového kódu. 
else!
pracovnik = 'Jan Makač' vyplata = 25_000 print('Pracovník:', pracovnik) je_dobry = input('Pracuje dobře? [a/n] ') # podmínka (vyhodnocení logického výrazu) if je_dobry == 'a' or je_dobry == 'A': # zde začíná podmíněný blok vyplata = vyplata + 5_000 # zde končí (skládá se z jediného příkazu) # tento kód se vždy vykoná print('Pracovník', pracovnik, 'dostane výplatu', vyplata, 'Kč.')
cislo = int(input('Zadej cenu v Kč: ')) # podmínka (vyhodnocení logického výrazu) if cislo % 100 == 0: # zde začíná podmíněný blok print('Cenu lze zaplatit ve stokorunách,') print('budeš jich potřebovat', cislo // 100, 'kusů.') else: # zde začíná alternativní blok print('Cenu nelze zaplatit pouze ve stokorunách,') print('budeš potřebovat', cislo // 100, 'kusů stokorun a') print('navíc', cislo % 100, 'Kč v mincích.') # tento kód se vždy vykoná print('Konec výpočtu.')
Pokud potřebujeme vytvořit více než dvě větve, můžeme použít řetězení podmínek if-else nebo s výhodou využít variantu s elif jako v následující ukázce.
hmotnost = float(input('Zadej hmotnost v kg: ')) # zřetězení podmínek pomocí elif if hmotnost >= 1000.0: # varianta 1 print('Hmotnost je', hmotnost * 0.001, 't,') elif hmotnost >= 100.0: # varianta 2 print('Hmotnost je', hmotnost * 0.01, 'q,') elif hmotnost >= 1.0: # varianta 3 print('Hmotnost je', hmotnost, 'kg,') elif hmotnost >= 0.001: # varianta 4 print('Hmotnost je', hmotnost * 1000, 'g,') else: # přítomnost bloku else je možná, nikoliv nutná # varianta 5 print('To neváží skoro nic,') # tento kód se vždy vykoná print('konec převodu.')
Řada (ne-li většina) algoritmů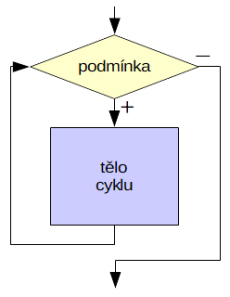 je založena na tom, že určitá sekvence příkazů se vykonává opakovaně, přičemž počet opakování se řídí nějakou podmínkou. Pokaždé před vstupem do těla cyklu se podmínka vyhodnotí. Při jejím splnění se tělo cyklu vykoná a znovu se vyhodnotí podmínka atd., v opačném případě se tělo cyklu přeskočí a cyklus končí. Situaci vidíte schematicky na přiloženém vývojovém diagramu.
je založena na tom, že určitá sekvence příkazů se vykonává opakovaně, přičemž počet opakování se řídí nějakou podmínkou. Pokaždé před vstupem do těla cyklu se podmínka vyhodnotí. Při jejím splnění se tělo cyklu vykoná a znovu se vyhodnotí podmínka atd., v opačném případě se tělo cyklu přeskočí a cyklus končí. Situaci vidíte schematicky na přiloženém vývojovém diagramu.
Počet opakování cyklu může být znám již před prvním vyhodnocením podmínky nebo přímo závisí na průběhu algoritmu. Obě situace jsou ukázány v příkladech níže. V každém případě by však mělo platit, že podmínka se po průchodu tělem cyklu může změnit. Není-li tomu tak, jedná se o „nekonečný“ cyklus a takový program samovolně nikdy neskončí! To svědčí o nějakém nedostatku v návrhu algoritmu nebo při jeho zpracování programátorem1).
# po určený počet let počítáme výnosy spoření castka = 10_000.0 # výchozí částka v Kč urok_sazba = 4.0 # roční úroková sazba v % roku = 10 # doba spoření print('Počáteční částka činí', castka, 'Kč.') rok = 0 # inicializace počítadla let while rok < roku: # cyklus proběhne 10krát # toto je tělo cyklu rok = rok + 1 # zvětšení počítadla # výpočet a výstup mezivýsledku castka = castka + castka * urok_sazba / 100.0 print('Po ', rok, ". roce činí částka", int(castka), 'Kč.')
# počítáme dobu spoření pro dosažení cílové částky castka = 10_000.0 # výchozí částka v Kč cilova_castka = 14_000.0 # cílová částka v Kč urok_sazba = 4.0 # roční úroková sazba v % print('Počáteční částka činí', castka, 'Kč.') rok = 0 # inicializace počítadla let while castka < cilova_castka: # počet opakování cyklu není předem znám # toto je tělo cyklu rok = rok + 1 # zvětšení počítadla # výpočet a výstup mezivýsledku castka = castka + castka * urok_sazba / 100.0 print('Po ', rok, ". roce činí částka", int(castka), 'Kč.') print('K naspoření cílové částky je třeba', rok, 'let.')
Efektivní způsob pro nalezení největšího společného dělitele dvou přirozených čísel je Eukleidův algoritmus.
# Eukleidův algoritmus pro nalezení NSD dvou čísel # vstup dat m = int(input('Zadej první přirozené číslo: ')) n = int(input('Zadej druhé přirozené číslo: ')) # krok 1: zajistíme, že n není větší z čísel if m < n: m, n = n, m # prohození čísel # krok 2: provádíme cyklus, dokud není n nulové while n != 0: r = m % n # krok 2a: zbytek po dělení m = n # krok 2b: nová hodnota m n = r # krok 2c: nová hodnota n # krok 3: dokončeno, vypíšeme výsledek print('NSD zadaných čísel je', m)
V některých situacích je obtížné umístit podmínku před vlastní tělo cyklu. Pak nám může pomoci příkaz break, který okamžitě ukončí právě probíhající cyklus a poté začne program vykonávat první příkaz za cyklem.
# výpočet aritmetického průměru zadaných čísel # zadávání končí prázdným vstupem # inicializace proměnných cisel = 0 soucet = 0.0 while True: # zdá se, že to je nekonečný cyklus vstup = input('Vstup čísla: ') if (vstup == ''): break # ale při prázdném vstupu se cyklus ukončí cisel = cisel + 1 # aktualizace poctu zadaných čísel soucet = soucet + float(vstup) # a jejich součtu # break skočí sem if cisel != 0: # nebudeme dělit 0, lze vypočítat aritmetický průměr print('Bylo zadáno čísel:', cisel) print('jejich průměr:', soucet / cisel) else: print('Nebyla zadána žádná čísla')
Běžně se kombinují oba způsoby (podmínka na začátku ošetřuje některé situace a podmíněný break jiné).
Při implementaci (zvláště rozsáhlejších a komplikovanějších) algoritmů může být vhodné dočasně některý blok příkazů nechat prázdný (s tím, že bude dokončen později). Příkazy jako if, else či while však nějaký blok vyžadují. V takovém případě si vypomůžeme zvláštním příkazem pass, který nic nedělá, ale má správnou syntaxi bloku příkazů.
if pocet > 10: pass # tady se nic nedělá else: pass # tady také ne
Po seznámení se s podmínkami a cykly naše možnosti řešení úloh závratně vzrostly. Uvědomte si také, že podmínky a cykly se mohou navzájem kombinovat a zanořovat (v podmíněném bloku se může vyskytnout cyklus a v něm ještě jeden atd.). Určitě je nyní třeba důkladněji si nabyté znalosti procvičit, dříve než se seznámíme s dalšími významnými rysy jazyka.
Ctrl a C.