Mini-statistika
Při opakovaném měření nějaké fyzikální veličiny obvykle nezískáme přesně stejné hodnoty. Matematická statistika nám dává návody, jak soubor naměřených dat vhodně charakterizovat jednou hodnotou a odhadnout úspěšnost takového popisu.
Budeme předpokládat, že máme k dispozici n naměřených hodnot x1, x2, …, xn a že přesnost a spolehlivost jednotlivých hodnot je srovnatelná. Nejpravděpodobnější hodnotu měřené veličiny určíme jako aritmetický průměr dle vzorce 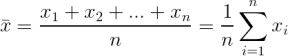 a pro výběrový rozptyl použijeme vztahy
a pro výběrový rozptyl použijeme vztahy 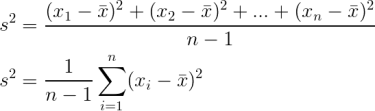 Výběrová směrodatná odchylka obvykle značená s (odmocnina z hodnoty výběrového rozptylu s2) nám říká, jakou chybou je zatížena jednotlivá naměřená hodnota. Jinými slovy, vypovídá o přesnosti našeho měření1).
Výběrová směrodatná odchylka obvykle značená s (odmocnina z hodnoty výběrového rozptylu s2) nám říká, jakou chybou je zatížena jednotlivá naměřená hodnota. Jinými slovy, vypovídá o přesnosti našeho měření1).
Je vhodné zmínit, že vztah pro směrodatnou odchylku s lze upravit do tvaru 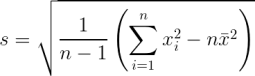 vhodnějšího pro strojové zpracování2). Není totiž potřeba ukládat si všechny naměřené hodnoty, stačí průběžně počítat součty jednotlivých hodnot a jejich čtverců. Konečné vyčíslení průměru a odchylky pak provedeme po zpracování poslední hodnoty.
vhodnějšího pro strojové zpracování2). Není totiž potřeba ukládat si všechny naměřené hodnoty, stačí průběžně počítat součty jednotlivých hodnot a jejich čtverců. Konečné vyčíslení průměru a odchylky pak provedeme po zpracování poslední hodnoty.
Hodnota s charakterizuje chybu jednotlivé měřené hodnoty, pro ohodnocení spolehlivosti aritmetického průměru používáme výběrovou směrodatnou odchylku aritmetického průměru 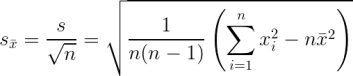 a výsledek měření fyzikální veličiny zapisujeme ve tvaru
a výsledek měření fyzikální veličiny zapisujeme ve tvaru 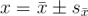 .
.
Více viz aritmetický průměr, směrodatná odchylka a učební text FO.
