Obsah
Jak velký je faktoriál?
Faktoriál n! přirozeného čísla n je funkce, kterou jsme poznali v kombinatorice jako počet všech permutací n–prvkové množiny. Setkat se s ním však lze v celé řadě odvětví matematiky.
Roste velmi rychle
Při výkladu jsme si ukázali, že funkce faktoriál se vzůstajícím n velmi rychle roste, vždyť například:
5! = 120
10! = 3 628 800
15! = 1 307 674 368 000
20! = 2 432 902 008 176 640 000
Možná jste zkoušeli počítat faktoriály i na běžné kapesní kalkulačce a došli jste k až číslu 69. Pro 70 a větší hodnoty hlásí většina kalkulaček chybu výpočtu. Je to dáno tím, že hodnota 70! je větší než 10100, což je maximální rozsah pro zobrazení na displeji.
Kolik tedy je např. 100!, 1000! nebo třebas 1 000 000! ? Samozřejmě můžeme mezi sebou postupně násobit sto, tisíc či milión čísel, což by nebylo příliš příjemné cvičení v elementární aritmetice, ale pomocí počítače je to docela dobře představitelná úloha. Např. zápis hodnoty 100! má v desítkové soustavě 158 číslic, zápis 1000! číslic 2568 a pro faktoriál miliónu bychom potřebovali již 5 565 709 číslic.
Jak rychle?
Pro naprostou většinu možných použití nám stačí vědět, že 100! ≈ 9,3326215444.10157. Nepotřebujeme tedy znát přesnou hodnotu, ale pouze rozumně přesný odhad. Přirozeně se tedy nabízí otázka, zda existuje spolehlivá možnost takový odhad získat.
Chování funkce faktoriál podrobně studovala již řada matematiků, kteří přinesli i odpověď (či odpovědi) na naši otázku. I gymnazista může sledovat alespoň první kroky v jejich úvahách.
Nejprve zhruba
Vzpomeneme si na vzorec pro logaritmus součinu1)
log(a.b) = log a + log b
a použijeme ho na faktoriál jako součin všech přirozených čísel až do n. Navíc si uvědomíme, že matematici mají přirozeně nejraději přirozené logaritmy (tj. takové, jejichž základem je Eulerova konstanta e). Dostaneme tedy
ln(n!) = ln(1.2. … .n) = ln 1 + ln 2 + … + ln n
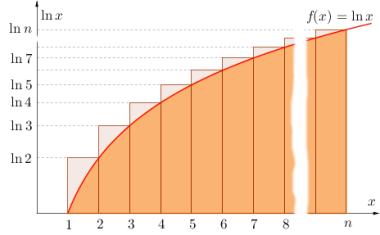 Součet na pravé straně si představíme jako celkovou plochu obdélníků (S) s jednotkovou šířkou a výškou rovnou postupně ln 1, ln 2 až ln n, které vhodným způsobem zakreslíme do grafu funkce f(x) = ln x (viz obrázek). Nyní vidíme, že pokud se nám podaří nějakým způsobem určit plochu pod grafem logaritmické funkce v rozsahu od 1 do n, máme první odhad pro logaritmus faktoriálu.
Součet na pravé straně si představíme jako celkovou plochu obdélníků (S) s jednotkovou šířkou a výškou rovnou postupně ln 1, ln 2 až ln n, které vhodným způsobem zakreslíme do grafu funkce f(x) = ln x (viz obrázek). Nyní vidíme, že pokud se nám podaří nějakým způsobem určit plochu pod grafem logaritmické funkce v rozsahu od 1 do n, máme první odhad pro logaritmus faktoriálu.
Žáci, kteří v maturitním ročníku navštěvují seminář z matematiky se naučí2), že přesně k tomuto účelu slouží určitý integrál. Logaritmus patří mezi elementární funkce3), které umíme snadno integrovat4). Učiníme-li tak v mezích od 1 do n, dostaneme ln(n!) = S ≈ n.ln n – n + 1. Po odlogaritmování už máme první odhad pro faktoriál n ve tvaru
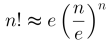
V každém případě již tento výsledek nám dává představu o rychlosti růstu funkce faktoriál. Pro dostatečně velká n vždy převáží nad libovolnou mocninnou či exponenciální funkcí.
Vylepšujeme odhad
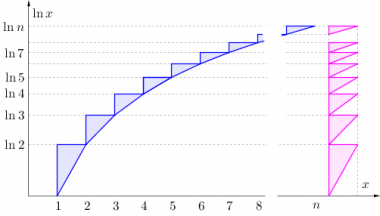 Pohledem na výše uvedený obrázek zjistíme, že velmi přímočaře dokážeme náš prvotní odhad ještě zpřesnit.
Pohledem na výše uvedený obrázek zjistíme, že velmi přímočaře dokážeme náš prvotní odhad ještě zpřesnit.
Části obdélníků ležící nad grafem funkce f(x) = ln x (což je právě to, o co jsme se při prvním odhadu „ošidili“) lze poměrně věrně aproximovat pomocí trojúhelníků (vyznačeny modře). Naložíme s nimi podle obrázku—vyrovnáme-li je nad sebe (viz nachová barva), vejdou se do obdélníka s šířkou rovnou jedné a výškou ln n. Jejich celková plocha je rovna 1/2.ln n. Zpřesněný odhad pak má tvar S ≈ n.ln n – n + 1/2.ln n + 1. Znovu obě strany odlogaritmujeme a získáme upřesněný odhad
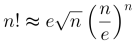
I z přiložených obrázků je zřejmé, že první aproximace poskytuje dolní odhad, právě popsané zpřesnění poskytne hodnotu mírně větší než je přesná.
Stirlingův vzorec
Sledování dalších kroků se s běžnými středoškolskými znalostmi stává již obtížnější5). Skotský matematik James Stirling dokázal upřesnit odhad do dnes široce používaného tvaru
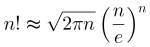
který se obyčejně nazývá Stirlingovým vzorcem. Řada historiků přírodních věd považuje jeho odvození za jeden z nejvýznačnějších počinů matematiky 18. století.
A dál a přesněji ...
Pokud by přesnost Stirlingova vzorce nebyla pro nějaký účel dostatečná, byla odvozena nekonečná řada korekčních členů. Při zahrnutí několika prvních z nich dostáváme pro odhad faktoriálu
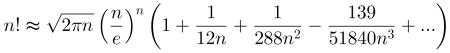 Existují i alternativní vyjádření odhadu, některá z nich zvláště vhodná např. pro použití v počítačových programech apod.
Existují i alternativní vyjádření odhadu, některá z nich zvláště vhodná např. pro použití v počítačových programech apod.
Porovnání
Abychom viděli a mohli posoudit, jak přesné jednotlivé aproximace jsou, vypočetla jsem několik hodnot a umístila je do tabulky. Pro snazší porovnání jsem všechna čísla uvedla v exponenciálním tvaru s mantisou zaokrouhlenou na 6 desetinných míst.
| n | n! | 1. odhad | 2. odhad | Stirlingův vzorec | Stirlingova řada |
|---|---|---|---|---|---|
| 5 | 1,200000.102 | 5,723637.101 | 1,279844.102 | 1,180192.102 | 1,200000.102 |
| 10 | 3,628800.106 | 1,234098.106 | 3,902561.106 | 3,598696.106 | 3,628800.106 |
| 15 | 1,307674.1012 | 3,641213.1011 | 1,410236.1012 | 1,300431.1012 | 1,307674.1012 |
| 20 | 2,432902.1018 | 5,874958.1017 | 2,627361.1018 | 2,422787.1018 | 2,432902.1018 |
| 100 | 9,332622.10157 | 1,011221.10157 | 1,011221.10158 | 9,324848.10157 | 9,332622.10157 |
Dá se říci, že již první odhad zhruba postihuje chování faktoriálu. Druhý odhad je výrazným zpresněním a Stirlingův vzorec již pro n větší než 10 poskytuje chybu aproximace menší než 1%, přičemž pro rostoucí n tato chyba nadále klesá. Aproximace uvedenou částí Stirlingovy řady je v zadaném oboru a rozsahu přesnosti nerozlišitelná od n!.
Literatura
- Podivuhodné křivky, počítání králíků a jiná matematická dobrodružství, Keith Ball, Argo/Dokořán (2011)
- Umění programování, díl 1. Základní algoritmy, D. E. Knuth, Computer press (2008)
