Údajně již učenci ve starověké Mezopotámii znali základy postupu, jak numericky vypočítat druhou odmocninu zadaného čísla pouze pomocí základních aritmetických operací. Každopádně to byl Sir Isaac Newton, který tuto metodu postavil na solidní matematické základy, proto se o ní často hovoří jako o Newtonově metodě.

Jedná se o iterativní postup, kdy začneme s prvotním odhadem výsledku a postupně jej upřesňujeme, dokud nejsme spokojeni s výslednou přesností. Budeme hledat druhou odmocninu x zadaného čísla a pomocí zpřesňování prvotního odhadu x₀ podle vzorce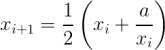 pro i = 0, 1, 2, … . Hodnoty x₁, x₂ atd. stále lépe aproximují požadovaný výsledek 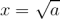. Jakmile dosáhneme požadované přesnosti, můžeme výpočet ukončit. Jako prakticky univerzální počáteční odhad x₀ se dá použít hodnota 1.

Popsaný algoritmus lze implementovat například takto:

odmocnina.py

# výpočet odmocniny Newtonovou metodou
 
# vstup čísla
a = float(input('Zadej kladné číslo: '))
 
x0 = 1.0 # počáteční odhad
 
presnost = 1.0e-14 # požadovaná relativní přesnost
iteraci = 0 # počítadlo iterací
 
# iterační cyklus
while True:
    x1 = 0.5 * (x0 + a / x0) # upřesnění odhadu
    iteraci = iteraci + 1 # aktualizace počítadla
    # vzhledem k velkému možnému řádovému rozmezí hodnot
    # je vhodné přesnost testovat v relativním měřítku
    if x0 * (1 - presnost) < x1 < x0 * (1 + presnost):
        break # požadovaná přesnost byla dosažena
    x0 = x1 # prohlásíme odhad za starý a opakujeme cyklus
 
# výpis výsledků
print('Odmocnina je přibližně    :', x1)
print('Přímo vypočtená hodnota   :', a ** 0.5)
print('Počet provedených iterací :', iteraci)

Pro porovnání je nakonec vytištěna i přímo vypočtená hodnota (pomocí vestavěného operátoru mocnění) a počet iterací potřebných k získání výsledku. Za připomínku stojí způsob vyhodnocení požadované přesnosti. Pokud během iteračního kroku dojde k relativní změně menší než přednastavená hodnota, výpočet je ukončen.

Pokud se zadané číslo vzdaluje hodnotě počátečního odhadu x₀ = 1, počet potřebných iterací pochopitelně narůstá, přesto ve velmi širokém rozsahu je výpočet prakticky okamžitě dokončen. Z toho plyne, že použitý iterativní postup je efektivním nástrojem k numerickému vyčíslení hodnoty druhých odmocnin celých i necelých kladných čísel.

Při zkoumání, jak se chová výpočet odmocniny v extrémních případech, zjišťujeme, že dosud dobře pracující algoritmus náhle selhává. Při zadání příliš velkých čísel (např. 1.0e+500) nedojde k dokončení výpočtu (program je v nekonečné smyčce) a naopak pro čísla příliš malá (jako 1.0e-500) program skončí s chybou dělení nulou. Pro vysvětlení je potřeba říci si něco více o vlastnostech datového typu float.

Na většině dnes běžně dostupných počítačů je datový typ float v Pythonu uložen jako 64bitová hodnota (tj. v 8 bytech paměti). Kódování hodnoty probíhá podle normy IEEE 754. Z hlediska programátora je vhodné vědět, že v nezáporném rozsahu dokáže kromě 0 uložit hodnoty přibližně 4,9.10^-324 až 1,79.10⁺³⁰⁸ (v rozsahu od 2,23.10^-308 do maxima s přesností na cca 15 platných číslic), obdobná pravidla platí v záporném směru číselné osy. Kromě toho dokáže uložit speciální hodnoty +∞ a -∞ a očekávaným způsobem s nimi počítat (např. ∞ + 2 se rovná ∞ apod.). Při nemožnosti provést výpočet (∞ - ∞ aj.) je výsledná hodnota NaN (Not a Number).

1.79e308                    # běžné číslo => 1.79e+308
1.80e308                    # nekonečno => inf
2.23e-308                   # běžné číslo => 2.23e-308
4.915e-324                  # běžné číslo (omezená přesnost) => 5e-324
2.0e-324                    # nula => 0.0
nekonecno = float('Inf')    # uložení nekonečna do proměnné, možné jsou i 
                            # tvary 'INF', 'inf', '+inf', 'infinity' apod.
nekonecno - nekonecno       # nekorektní výpočet => nan
1 / nekonecno               # => 0.0
minus_nek = float('-Inf')   # uložení mínus nekonečna do proměnné

Vyzbrojeni novými poznatky již můžeme vysvětlit výše zmíněná pozorování. Pro velká vstupní čísla je do proměnné a vlastně uloženo +inf, což se postupně přenese i do x1 a x0. V následujícím upřesnění odhadu pak selže vyhodnocení a / x0 (výraz ∞/∞ vede k výsledku NaN). Proměnné x0 i x1 tak získají hodnotu NaN a podmínka pro přerušení cyklu nemůže být nikdy splněna.

Pro extrémně malá čísla (např. pro již zmíněných 1.0e-500) dojde po více než 1000 průchodech cyklu ke snížení odhadu na tak malé číslo, že je interpretováno jako nula. Při následném výpočtu podílu a / x0 pak samozřejmě dojde k chybě při dělení nulou a okamžitému ukončení programu.

Poučení
Již dříve jsme narazili na konečnou přesnost datového typu float, nyní vidíme i další jeho limity. Ve většině případů nám tento datový typ slouží prakticky stejně dobře jako reálná čísla v matematice (ostatně k tomuto účelu byl vytvořen). Můžeme se však dostat do situace, kdy program přestává poskytovat očekávané výsledky, přestože z matematického hlediska je „všechno správně“. Pak je nutno uvážit i vlastnosti použitého datového typu!

Analogicky k druhé odmocnině je možné odvodit i příslušné vzorce pro výpočet vyšších (n tých) odmocnin (n = 3, 4, atd.) 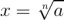, které lze souhrnně zapsat výrazem 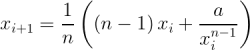s tím, že x₀ je i zde vhodný prvotní odhad (opět např. hodnota 1). Výše uvedený vztah pro druhou odmocninu je speciálním případem pro n = 2. Úprava zdrojového kódu programu je velmi přímočará a není třeba ji přímo uvádět.