Výpočet odmocnin - upřesnění odhadu
Při výpočtu odmocnin Newtonovou metodou jsme poměrně velmi úspěšně vystačili s prvotním odhadem x0 = 1,0. Následující iterační cyklus nás s argumentem a v celém rozsahu datového typu float nakonec dovedl k dobré aproximaci hledané odmocniny. Není přitom nijak překvapivé, že při větším rozdílu mezi a a prvotním odhadem narůstá počet iterací k dosažení požadované relativní přesnosti. Platí to jak pro velká a (postupně rostoucí až k limitu 10+308) tak pro malá (ale stále kladná) a postupně klesající k 0. Pro limitní vstupy přesáhl počet iterací v našem případě hodnotu 500.
Lepší prvotní odhad
Zkusme nyní prozkoumat, zda bychom pro a „vzdálené“ od hodnoty 1,0 nemohli jednoduše vylepšit prvotní odhad a tím celkově urychlit celý výpočet odmocniny.
Jednou z myšlenek, které se nabízí k vyzkoušení, je učinit velmi hrubý řádový odhad (z hlediska desítkové soustavy), jak je naznačeno v tabulce1):
| rozsah od | rozsah do | střed | odhad x0 |
|---|---|---|---|
| 10-5 | 10-3 | 10-4 | 10-2 |
| 10-3 | 10-1 | 10-2 | 10-1 |
| 10-1 | 10+1 | 100 | 100 |
| 10+1 | 10+3 | 10+2 | 10+1 |
| 10+3 | 10+5 | 10+4 | 10+2 |
| a tak podobně pro menší i větší argumenty | |||
Implementace takového zpřesnění odhadu je přímočará pomocí jednoduchého cyklu (přitom není podstatné, jakým způsobem zahrneme krajní body intervalu).
# výpočet odmocniny Newtonovou metodou # vylepšení počátečního odhadu, argument je v proměnné a x0 = 1.0 # začneme od 1 odhadu = 0 # počítadlo úprav počátečního odhadu prac = a # pomocná pracovní proměnná if prac >= 1.0: # napravo od 1 while prac >= 10: x0 = 10 * x0 # jeden řád v odhadu prac = prac / 100 # na dva řády argumentu odhadu = odhadu + 1 # aktualizace počítadla else: # nalevo od 1 while prac < 0.1: x0 = 0.1 * x0 # jeden řád v odhadu prac = prac * 100 # na dva řády argumentu odhadu = odhadu + 1 # aktualizace počítadla # počáteční odhad je v proměnné x0
Zbytek programu odmocnina.py2) zůstal zachován (celý program je odmocnina2.py), proměnná odhadu slouží k počítání cyklů při získání počátečního odhadu a spolu s počítadlem iteraci následujích newtonovských iterací nám poslouží k posouzení účinnosti upraveného řešení.
Porovnání
Budeme spouštět oba programy (s počátečním odhadem 1,0 i upřesněným odhadem) v širokém rozmezí hodnot a (zastoupených rovnoměrně v logaritmickém měřítku od 10-100 do 10+100) a získaná data graficky znázorníme. 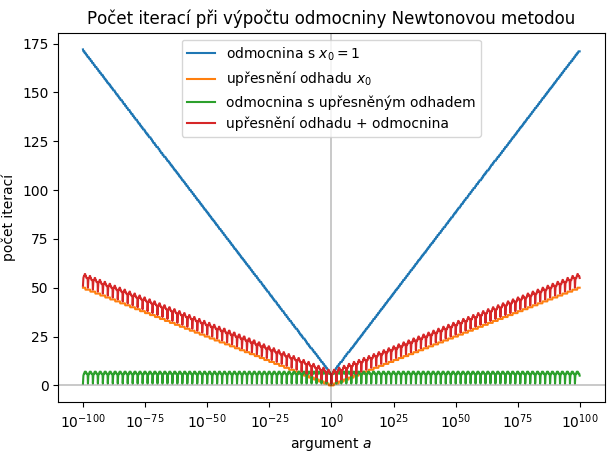 Modrá křivka popisuje chování programu
Modrá křivka popisuje chování programu odmocnina.py (tj. s počátečním odhadem x0 = 1,0). Je vidět, že logaritmické měřítko vodorovné osy je zvoleno vhodně a že v tomto zobrazení počet potřebných iterací pro výpočet v podstatě lineárně roste při vzdalování se od hodnoty 1,0 (to znamená, že počet iterací je zhruba úměrný | log a |).
Ostatní křivky v grafu se týkají programu odmocnina2.py s vylepšením počátečního odhadu. Oranžová schodovitá křivka vypovídá o počtu cyklů potřebných k získání počátečního odhadu. S jeho pomocí je počet potřebných iterací Newtonovy metody v celém rozsahu omezen hodnotou 10 - to je zelená křivka. Konečně červená závislost je celkový počet provedených cyklů (tj. součet oranžových a zelených datových bodů). Snadno odhadneme, že jeden průchod cyklem při získání odhadu není náročnější než samotná newtonovská iterace, tedy celková hodnota je spíše mírně nadhodnocena.
Výsledek
Z grafu je zřejmé, že lepší prvotní odhad vylepší výkonnost celého výpočtu. Pokud budeme relativně blízko 1,0 (řekněme v intervalu od 10-6 do 10+6), tak je zrychlení nevýznamné (ale nedochází ani ke zpomalení). Pokud lze očekávat, že při opakovaném využití algoritmu bude významná část vstupních argumentů mimo uvedený rozsah3), má lepší počáteční odhad smysl a lze očekávat asi dvoj- až trojnásobné zrychlení výpočtu odmocniny.
V každém případě je však na místě znovu konstatovat, že Newtonova metoda pro výpočet druhé odmocniny funguje velmi dobře.
Poučení
Cílem tohoto článku bylo ukázat, že je vhodné zamýšlet se nad možnostmi vylepšení algoritmů, zkoušet různé nápady4) a že má smysl studovat chování algoritmů v různých situacích. Určitě je výhodné umět popsat složitost výpočtu matematicky, často (a někdy to je jediná schůdná cesta5)) lze získat prokazatelné výsledky na základě experimentálních dat (tj. měření). Tím získáme podklady pro určení částí, které má smysl optimalizovat a které nikoliv.
