Mersennova prvočísla

Přirozená čisla o jednu menší než celočíselná mocnina 2 nazveme Mersennova čísla, Mersennovo číslo M_n má tedy tvar

pro n = 1, 2, … . Máme tedy M₁ = 1, M₂ = 3, M₃ = 7, atd. V některých případech se jedná o prvočísla (např. M₃, pak hovoříme o Mersennových prvočíslech), v jiných případech o čísla složená (např. M₁₁ = 2047 = 23.89).

Čislo 2^74 207 281 − 1, které má více než 22 miliónů desetinných cifer, bylo v době psaní této stránky největším známým prvočíslem vůbec. Dne 3. ledna 2018 bylo ohlášeno nalezení již 50. Mersennova prvočísla 2^77 232 917 − 1 s více než 23 milióny číslic a 21. prosince téhož roku bylo oznámeno již 51. prvočíslo 2^82 589 993 − 1 (24 862 048 desetinných číslic). Hledání těchto prvočísel koordinuje projekt GIMPS. Není dokázáno, zda existuje nekonečně mnoho Mersennových prvočísel.

Vyzbrojeni algoritmem na ověřování prvočíselnosti můžeme zkusit zkoumat, která Mersennova čísla jsou prvočísly. V cyklu od 1 do nějaké rozumné meze tedy vytváříme testovaná čísla a aplikujeme na ně náš algoritmus. Pro jednotlivá čísla vypisujeme, zda se jedná o prvočíslo nebo uvedeme jeho rozklad na důkaz toho, že se jedná o číslo složené.

mersenne1.py

# hledání Mersennových prvočísel M_n = 2^n - 1
# pro n od 2 do 60
 
n = 2 # počítadlo
mocnina2 = 4 # průběžně si pamatujeme mocninu 2
# testujeme kandidáty v určeném rozsahu
while n <= 60:
    cislo = mocnina2 - 1 # číslo je rozhodně liché
 
    # není potřeba testovat dělitelnost 2!
    # testování lichých dělitelů
    delitel = 3 
    # testování jednotlivých dělitelů v cyklu
    while delitel * delitel <= cislo: # POZOR: musí být <=
        if cislo % delitel == 0: # test dělitelnosti
            break # dělitel nalezen, není třeba dále testovat
        delitel = delitel + 2 # další lichý dělitel
    # konec testování lichých dělitelů
 
    if delitel * delitel > cislo: # výpis nalezeného prvočísla
        print('M', n, '=', cislo, 'je prvočíslo')
    else:
        print('M', n, '=', cislo, '=', delitel, '*', cislo // delitel)
 
    n = n + 1 # jdeme na další číslo
    mocnina2 = mocnina2 * 2 # aktualizujeme mocninu 2

V testování dělitelů jsme si mohli dovolit přeskočit 2, protože Mersennovo číslo nikdy nemůže být sudé. Mocniny 2 vytváříme průběžně násobením 2, předchozí mocninu si pamatujeme ve zvláštní proměnné. Po ukončení vnitřního cyklu vždy vyhodnotíme podmínku a vypíšeme výsledek.

Ukazuje se, že tímto programem snadno a rychle otestujeme čísla do indexu 60. Při pokusu o testování M₆₁ však výsledek dlouho nedostáváme, proto pravděpodobně sáhneme k násilnému ukončení programu.

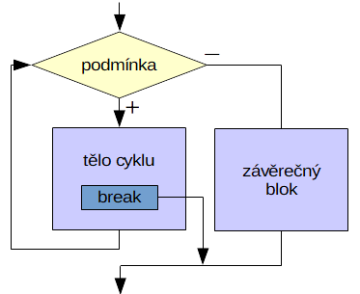Na tomto místě učiníme malou odbočku a ukážeme si jednu další možnost, kterou nám v Pythonu dává cyklus while. Můžeme totiž i pro cyklus definovat závěrečný blok else, který se vykoná po ukončení vlastního cyklu. Ptáte se možná, k čemu to je dobré? Jde o to, že pokud je provádění cyklu přerušeno příkazem break, tento závěřečný blok se přeskočí. To znamená, že else blok se provede pouze v případě ukončení cyklu na základě nesplnění úvodní podmínky. Snad je to dobře patrné i z vývojového diagramu.

V některých případech nám může použití bloku else ušetřit dodatečnou podmínku, jako v příkladu níže, nebo zvýšit přehlednost kódu. Na druhou stranu se lze poměrně snadno bez takové možnosti obejít, ostatně řada jiných programovacích jazyků jako C/C++, Pascal, Java, C# aj. ekvivalentní konstrukci neposkytují.

mersenne2.py

# hledání Mersennových prvočísel M_n = 2^n - 1
# pro n od 2 do 60
 
n = 2 # počítadlo
mocnina2 = 4 # průběžně si pamatujeme mocninu 2
# testujeme kandidáty v určeném rozsahu
while n <= 60:
    cislo = mocnina2 - 1 # číslo je rozhodně liché
 
    # není potřeba testovat dělitelnost 2!
    # testování lichých dělitelů
    delitel = 3 
    # testování jednotlivých dělitelů v cyklu
    while delitel * delitel <= cislo: # POZOR: musí být <=
        if cislo % delitel == 0: # test dělitelnosti
            print('M', n, '=', cislo, '=', delitel, '*', cislo // delitel)
            break # dělitel nalezen, není třeba dále testovat
        delitel = delitel + 2 # další lichý dělitel
    # konec testování lichých dělitelů
    else: # výpis nalezeného prvočísla
        print('M', n, '=', cislo, 'je prvočíslo')
 
    # break skočí až sem
    n = n + 1 # jdeme na další číslo
    mocnina2 = mocnina2 * 2 # aktualizujeme mocninu 2

Uvedli jsme, že výše uvedený program nám v rozumně krátké době nezodpověděl, zda M₆₁ je prvočíslo. Není to až tak překvapivé, protože 2⁶¹ ≈ 2,306.10¹⁸ a pro prokázání prvočíselnosti je potřeba otestovat více než tři čtvrtiny miliardy dělitelů. Již dříve jsme učinili některé zkušenosti, že tam, kde nestačí hrubá síla, se můžeme zkusit obrátit s prosbou o pomoc na matematiku. Ta nás naštěstí ani v tomto případě nezklame.

Není až tak obtížné dokázat, že Mersennovo číslo M_n může být prvočíslem jen pro prvočíselné n, v opačném případě je vždy složeným číslem. Již to nám vydělí celou řadu kandidátů. Velký krok vpřed je pak test odvozený Lucasem a následně vylepšený Lehmerem, který dokáže jednoznačně rozhodnout o prvočíselnosti M_n, pokud je n libovolné prvočíslo (s výjimkou 2). Test je poměrně jednoduchý¹⁾, stačí vytvořit posloupnost podle těchto pravidel:

• s₀ = 4,
• s_i = (s_i-1.s_i-1 - 2) mod M_n pro i = 1, 2, …, n - 2. Operace modulo k znamená zbytek po celočíselném dělení k.

Nakonec otestujeme poslední člen posloupnosti (tj. s_n-2). Je-li nulový, pak M_n je prvočíslo, je-li libovolný nenulový, jde o číslo složené.

S pomocí nově nabytých znalostí pak snadno a rychle určíme, že M₆₁ je opravdu prvočíslo²⁾.

lucas_lehmer.py

# Lucas-Lehmerův test, zda Mersennovo číslo M_61 = 2^61 - 1
# je prvočíslo
# podmínky testu jsou splněny - exponent 61 je liché prvočíslo
 
exponent = 61
cislo = 2 ** exponent - 1 # zkoumané Mersennovo číslo
 
s = 4 # počátek LL posloupnosti
krok = 0 # počítadlo kroků
while krok < exponent - 2:
    s = (s * s - 2) % cislo # další člen LL posloupnosti
    krok = krok + 1 # aktualizace počítadla
 
# závěrečný test a tisk výsledku
if s == 0:
    print('M', exponent, '=', cislo, 'je prvočíslo')
else:
    print('M', exponent, '=', cislo, 'je složené číslo')

Nakonec poskládáme všechny díly skládačky do programu na hledání Mersennových prvočísel s využitím Lucas-Lehmerova testu. Kromě n = 2 budeme procházet jen liché exponenty n. Klasickým algoritmem zkontrolujeme prvočíselnost n a v kladném případě postoupíme k Lucas-Lehmerovu testu (viz vývojový diagram). Možný výsledek je v programu mersenne3.py. S jeho pomocí lze i na běžném již dosti vousatém počítači nalézt všechna Mersennova prvočísla až do indexu 3500 během necelé půl minuty! To znamená všechna M_n, která mají méně než 1000 číslic v dekadickém zápisu! Vzpomeneme-li si na naše původní obtíže s indexem 61, jedná se o úžasný výsledek.

Naše nové zkušenosti tak znovu vysvětlují velmi úzký vztah mezi teoretickou informatikou a matematikou. Je snad na místě také podotknout, že studium prvočísel, jejich testování, hledání faktorizace čísel a příbuzné úlohy jsou stále v centru pozornosti vědců i programátorů. Mají totiž úzký vztah ke konstrukci šifrovacích schémat a bezpečnosti informací.

Na závěr této kapitoly dovolte malou poznámku k implementaci celočíselného typu int v jazyku Python. Bezstarostně a s maximálním pohodlím jsme výše prováděli aritmetické výpočty s poměrně velkými nezápornými čísly bez jakékoliv ztráty přesnosti (důsledně jsme používali datový typ int). Takový komfort většina programovacích jazyků ve své základní výbavě neposkytuje. Naopak je typické, že existují celočíselné typy pevné velikosti (často ve znaménkové a neznaménkové formě), např. 16bitový znaménkový integer obvykle pojme hodnoty od -32 768 do +32 767, 32bitový neznaménkový od 0 do 4 294 967 295 apod. Ty většinou odpovídají datovým typům, se kterými dokáže pracovat mikroprocesor na nejnižší úrovni. Při výpočtech pak musíme dávat pozor na to, zda jsme konkrétní datový typ správně zvolili a zda se výsledky operací vejdou do určeného rozsahu. Částečně podobné problémy jsme řešili u typu float. Pro celočíselné výpočty v „neomezeném“ rozsahu se pak v ostatních jazycích používají speciální nadstavbové knihovny.