Poté, co jsme se poměrně úspěšně vyrovnali s výpočtem odmocnin, obrátíme svou pozornost k úkolu, jak vypočítat hodnotu nejběžnějších matematických konstant e (Eulerova čísla) a π jen pomocí základních aritmetických operací. Víme, že se jedná o iracionální čísla¹⁾, proto jakýkoliv desetinný zápis bude vždy pouze přiblížením.

Matematici odvodili řadu postupů, jak k hodnotě těchto konstant dospět. Mnoho z nich je založeno na součtu nekonečných řad. Přestože v matematice probíráme posloupnosti a řady až ke konci předposledního ročníku, je pro nás pravděpodobně intuitivně přijatelné, že za jistých podmínek se postupným přičítáním stále menších položek můžeme bez omezení blížit k nějaké konečné hodnotě. Pak má nekonečný součet řady členů a_n 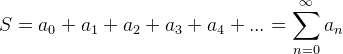dobře definovaný smysl.

Pro výpočet Eulerova čísla e máme nekonečnou řadu 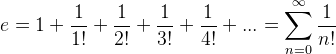složenou ze zlomků, kde ve jmenovatelích figurují faktoriály přirozených čísel (z řady důvodů je vhodné prohlásit 0! = 1). Faktoriál je velmi rychle rostoucí funkce, proto velikost jednotlivých členů s rostoucím n rychle klesá, což je pro výpočet výhodné.

Z hlediska výpočtu jednotlivých členů je vhodné si povšimnout, že nemusíme vždy počítat celý faktoriál. Mezi dvěma následujícími členy totiž pro n ≥ 1 platí 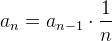a to při výpočtu využijeme²⁾. Program pro výpočet e se kromě úvodních inicializací skládá z jednoduchého cyklu, ve kterém počítáme další člen a přičítáme jej do výsledku, a závěrečného tisku výsledků.

euler.py

# výpočet Eulerova čísla e
# součtem nekonečné řady e = 1 + 1/1! + 1/2! + 1/3! + ...
 
print('Výpočet Eulerova čísla')
print('--------------------------')
vysledek = 1.0 # proměnná pro součet členů
clen = 1.0 # hodnota a_0
print('a', 0, '=', clen) # tisk členu
n = 1 # počítadlo členů řady
presnost = 1e-16 # požadovaná přesnost
 
# počítáme další členy do dosažení požadované přesnosti
while clen > presnost:
    clen = clen / n # další člen s využitím předchozího
    vysledek = vysledek + clen # přičteme do výsledku
    print('a', n, '=', clen) # tisk mezivýsledku
    n = n + 1 # jdeme na další člen
 
# tisk výsledků
print('--------------------------')
print('e =', vysledek)
print('členů:', n)

Vzhledem k vlastnostem datového typu float jsme zvolili jako hraniční hodnotu pro velikost členu 1.10^-16. Po spuštění zjistíme, že součet 19 členů nám poskytuje výsledek, který se od skutečné hodnoty e = 2,71828 18284 59045 23536… liší až na 16. desetinném místě.

Pro výpočet π (též Ludolfova čísla) existuje mnoho vztahů, my nyní použijeme nekonečnou řadu 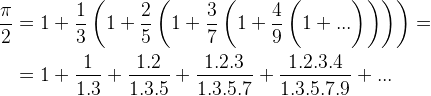často spojovanou s Newtonovým jménem. Z hlediska programátora je výhodnější vycházet z druhého tvaru. Je zřejmé, že členy řady neklesají tak rychle jako u Eulerova čísla, proto pro dosažení stejné přesnosti očekáváme potřebu většího počtu členů. V čitateli členů stojí faktoriály, ve jmenovatelích pak součiny lichých čísel. Díky platnosti 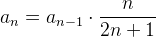pro n ≥ 1 se nám výpočet následujícího členu opět zjednoduší. Program je velmi podobný předchozímu, stačí vlastně jen změnit výpočet následujícího členu v cyklu a nezapomenout na konci vynásobit výsledek 2 (součet řady je π / 2).

cislo_pi.py

# výpočet Ludolfova čísla
# součtem řady pi/2 = 1 + 1/1.3 + 1.2/1.3.5 + 1.2.3/1.3.5.7 + ...
 
print('Výpočet Ludolfova čísla')
print('--------------------------')
vysledek = 1.0 # proměnná pro součet členů
clen = 1.0 # hodnota a_0
print('a', 0, '=', clen) # tisk členu
n = 1 # počítadlo členů řady
presnost = 1e-16 # požadovaná přesnost
 
# počítáme další členy do dosažení požadované přesnosti
while clen > presnost:
    clen = clen * n / (2 * n + 1) # další člen s využitím předchozího
    vysledek = vysledek + clen # přičteme do výsledku
    print('a', n, '=', clen) # tisk mezivýsledku
    n = n + 1 # jdeme na další člen
 
# tisk výsledků
print('--------------------------')
print('pi =', 2 * vysledek)
print('členů:', n)

Po spuštění zjišťujeme, že až člen a₅₁ je menší než předepsaná hranice a výsledek se shoduje se správnou hodnotou 3,14159 26535 89793 23846… v 14 desetinných místech, vyšší přesnosti již brání zaokrouhlovací chyby.

Bylo nalezeno mnoho jiných vyjádření pro π pomocí nekonečné řady, která konvergují mnohem rychleji. Jedním ze zajímavých vztahů je Baileyho-Borweinův-Plouffeův vzorec 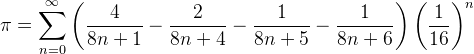odvozený v roce 1995. Není sice rekordmanem v rychlosti konvergence, ale umožňuje provést výpočet libovolné číslice nekonečného rozvoje (zapsaného v hexadecimální soustavě) bez znalosti předchozích!

Číslo π bylo pomocí superpočítačů vypočteno již na více než 10¹² platných číslic!